
Art et fractales : découverte d’un monde infini
Fractales… Derrière ce nom étrange se cache un univers infini, mêlant art et mathématiques. Laissez-vous guider dans le monde étonnant d’objets grandioses !
Voici la première partie d’un dossier (in)complet dédié aux fractales. Chaque semaine, retrouvez un épisode à ce sujet. Aujourd’hui, présentation du concept et premiers pas vers l’inconnu !
Une fractale ?
Sans entrer dans des détails trop complexes, voici une rapide définition de ce qu’est une fractale :
Venant du latin « fractus » (brisé ou irrégulier), une figure fractale est un objet géométrique pouvant s’apparenter à une poupée russe à l’infini. Autrement dit, qu’importe l’endroit où l’on zoome et le niveau de ce rapprochement, on pourra observer le même motif. La forme se reproduit à des échelles différentes, sans fin.
Évidemment, « à l’infini » n’est pas toujours possible, mais l’idée est là. On retrouve ce principe dans la nature ; un exemple assez parlant est le chou romanesco :

On observe bien la répétition du motif d’un splendide vert clair : les excroissances sont formées d’ensembles similaires plus petits, et ainsi de suite. Ce n’est évidemment pas le seul exemple naturel : vos poumons et leurs alvéoles peuvent aussi être considérés fractales.
L’objet de ce type le plus connu porte le nom de Benoît Mandelbrot, inventeur du terme, en 1974.

Ce brave monsieur avait poussé un cri de désespoir face à ses consorts qui étudiaient alors le monde grâce à la théorie des grands nombres, laissant de côté un bon nombre de phénomènes (comme la forme des nuages, des fleuves…). N’empêche qu’après sa gueulante, on s’est un peu plus intéressé aux objets bizarres s’empoussiérant jusqu’alors dans les tiroirs des mathématiciens.
Et l’art, dans tout ça ?
De nombreux artistes s’intéressent aux fractales. Le mouvement a pris de l’ampleur aux alentours de 1980, quelques années après la définition de Mandelbrot. La période coïncide avec l’amélioration des capacités de calcul des ordinateurs, permettant la création d’images complexes via des procédés algorithmiques. Les premières fractales ainsi crées l’étaient en 2D (tristesse et platitude).
Il a fallu attendre 2009 pour que soit produite la première fractale en 3D, le Mandelbulb (par Daniel White et Paul Nylander, avec l’aide de différents utilisateurs des Fractal Forums). Tirant son nom de la figure présentée précédemment, elle a ouvert la voie à l’imagerie 3D.
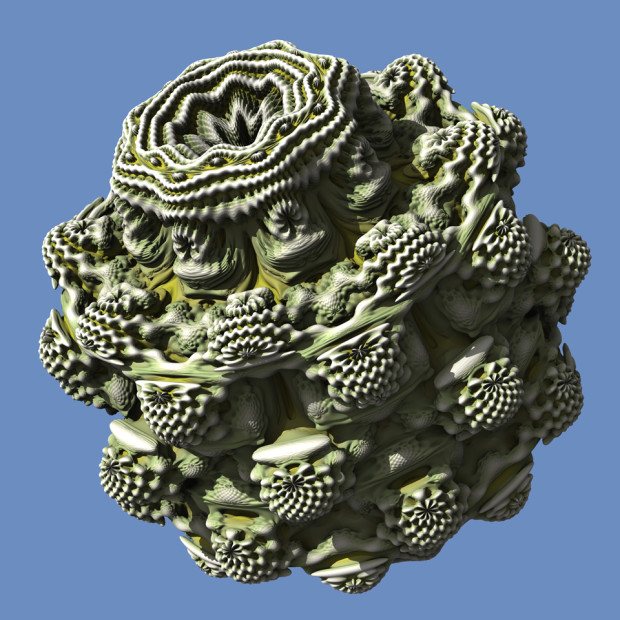
… effectivement, on a vu plus sexy. Cela dit, cela a demandé 2 ans de tests et d’équations mathématiques pour y arriver, alors un peu de respect.
Depuis, les logiciels permettant de produire de magnifiques créations se sont multipliés et la qualité visuelle des fractales n’a jamais été aussi impressionnante ! Nous verrons ça plus en détail dans les prochains articles sur le sujet. En attendant, et comme je suis magnanime, voici un petit ensemble de créations par divers artistes…



Cela fait envie, pas vrai ? Comme vous pouvez le voir, une certaine liberté des formes a été prise, le motif de base se répétant plus ou moins à l’infini, selon les choix de l’artiste. Le degré d’abstraction est fort, ce qui n’enlève rien à ces œuvres hautes en couleurs, où l’on se laisser plonger…
On se retrouve la semaine prochaine, le 30 janvier, pour découvrir le premier artiste de la série !
D’ici là, n’hésitez pas à suivre l’artboratoire sur Facebook et/ou Twitter, pour ne pas rater la suite ! De même, si vous avez des remarques, les commentaires vous attendent à bras ouverts ; toute critique est bonne à prendre.






Commentaires
Vous avez sûrement un avis à partager !
Les champs marqués par un astérisque (*) sont obligatoires.